一、蒙特卡洛方法介绍

（一）蒙特卡洛方法是什么？

在现实生活中，很多问题都存在不确定性，如彩票是否中奖、机构是否违约及股票未来价格走势等，单个的随机事件我们不可预测，但随机大量的群体行为，却可能是精确可知的，这就是概率世界的魅力，在偶然中隐含着必然。蒙特卡洛方法的有效性正是建立在大数定律的基础上，通过模拟一个大量重复的随机过程，以不断接近真实的结果。

蒙特卡洛方法又称随机抽样或统计试验方法，以概率和统计学理论为基础，利用随机数来产生基于一定分布假设的数字序列，进而解决各种计算问题。将所求解的问题同一定的概率模型相联系，并借助计算机实现统计模拟或抽样，以获得问题的近似解。为象征性地表明这一方法的概率统计特征，故借用赌城蒙特卡洛命名。

（二）关于蒙特卡洛的示例：估算圆周率

关于蒙特卡洛模拟的经典示例是用该方法来估算圆周率π。过程如下：

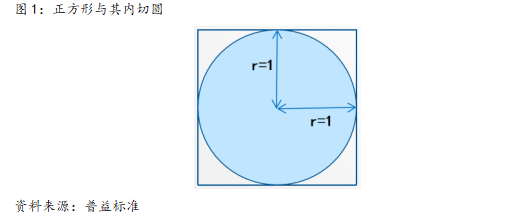
如图所示，为单位圆以及与之相切的正方形，由于内切圆的直径与正方形边长相等，因此二者的面积分别为：

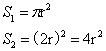
其中，S1代表圆的面积，S2代表正方形的面积，r代表圆的半径。

二者面积之比为：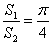

现在，通过设置计算机程序，随机在正方形内投掷尽可能多的点，如1万个，即得到下图：

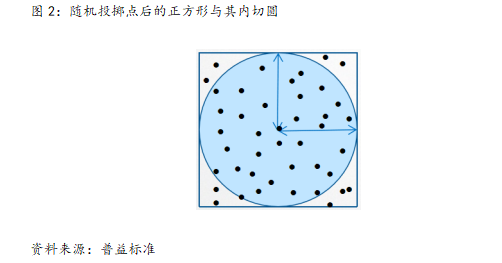
所谓“随机”，即正方形内任何一点得到的概率是一样的。每次当点被投入圆内时，进行计数，统计1万个点中投到圆内的数量N。则有近似的等价关系：

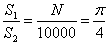
由此，即可得到近似π的值。同时，随着模拟次数的增多，模拟出来的圆周率π就会越精确。

蒙特卡洛模拟在众多领域都有着广泛的应用，如金融工程学、宏观经济学、生物医学、气象学、天文学和粒子物理学等。当在预测或估算过程中面临重大不确定性时，蒙特卡洛模拟可能被证明是一种很好的解决方案。

二、蒙特卡洛用于预测资产价格

下面将应用蒙特卡洛方法预测股票的价格：

把股价简单表示为：

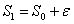
上式中，S1表示当天的股价，S0表示上一天的股价，ε表示当天的股价波动。

此时，预测股价的关键是股价的波动，股价的波动可以理解为是一个随机数，即取值不确定的数。比如某股票的股价S0＝10，此时如果随机生成第一个随机数，如ε1=0.3，那么S1=10.3，这样就往前走了一步，接下来再随机生成一个随机数ε2=－0.4，则S2＝9.9，按照同样的方法，往前走100步，就可以找到100天之后的股价，这样就找到了这100天股价波动的一条路径。显然，该股票实际的股价走势与我们所估计的并不一致，正由于条条大道通罗马，未来是有无数可能性，而这个路径是模拟出来的，只是未来众多可能性的一种。在此基础上，可以用同样的方法模拟出1万条甚至更多的路径，那么在第100天的时候，就会有1万个数据，此时最简单的，可以求平均数，作为对未来股价的预测。

实际上，随机数的生成并不是完全无规律的，一般做蒙特卡洛模拟先要根据历史数据的特征假设随机数的分布。实务中，常用几何布朗运动模拟股票价格。

（一）公式

随机过程St在满足以下随机微分方程的情况下被认为遵循几何布朗运动：

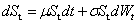
上式中，St表示资产价格，Wt是一个维纳过程，或者说是布朗运动（随机数），μ代表预期收益率，σ代表波动率。

给定初始值S0，根据伊藤引理，上面的随机微分方程进行推导后，可以得到：

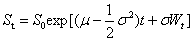
即资产价格变动有两个组成部分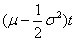：代表资产价格的漂移项(Drift，即恒定的定向运动)，以及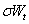代表市场波动（Volatility）的随机输入。

（二）回测分析

1.模型构建

选用资产：沪深300指数（指数代码：000300）近500个交易日的收盘价，作为历史数据

预测期间：从2020年7月13日开始（指数初始值为4753点），未来1000个交易日的指数走势

漂移项：平均日回报-方差/2，其中：日回报=ln（当日价格/上一日价格）

随机变量：波动率×正态分布随机数

2.模拟结果

（1）10个预测轨迹

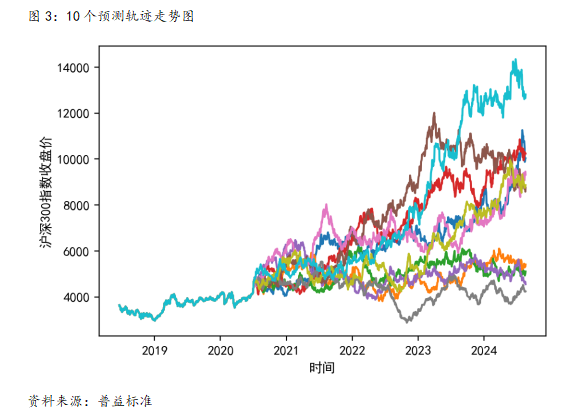
回测结果：1000个交易日后，预期指数平均值为7931点，预期年化收益为12.96%。

（2）1000个预测轨迹

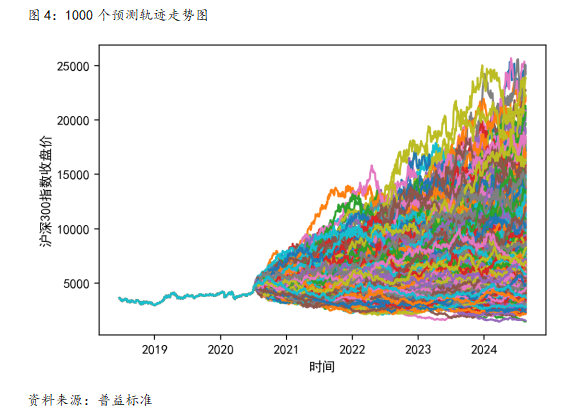
回测结果：1000个交易日后，预期指数平均值为8083点，预期平均年化收益为13.47%，预期年化收益的80%置信区间为0.95%~22.69%，预期年化收益的95%置信区间为-19.41%~29.87%。

欲获取报告全文，请联系我们购买